Activité 5 - Un peu de détente avec le module turtle

L’une des grandes qualités de Python est qu’il est extrêmement facile de lui ajouter de nombreuses fonctionnalités par importation de divers modules.

Pour illustrer cela, et nous amuser un peu avec d’autres objets que des nombres, nous allons explorer un module Python qui permet de réaliser des « graphiques tortue », c’est-à-dire des dessins géométriques correspondant à la piste laissée derrière elle par une petite « tortue » virtuelle, dont nous contrôlons les déplacements sur l’écran de l’ordinateur à l’aide d’instructions simples. Activer cette tortue est un vrai jeu d’enfant. Plutôt que de vous donner de longues explications, nous vous invitons à essayer tout de suite :

Créez un fichier nommée first.py qui contient le code suivant :

from turtle import *
forward(120)
left(90)
color('red')
forward(80)

Commandes de base

Les commandes de base pour déplacer la tortue et lui faire afficher des choses sont les suivantes :

reset() On efface tout et on recommence

goto(x, y) Aller à l’endroit de coordonnées x, y

forward(distance) Avancer d’une distance donnée

backward(distance) Reculer

circle(r) Dessiner un cercle de rayon r

up() Relever le crayon (pour pouvoir avancer sans dessiner)

down() Abaisser le crayon (pour recommencer à dessiner)

color(couleur) modifier la couleur du trait (on peut utiliser une chaîne prédéfinie :’red’, ’blue’... )

bgcolor(couleur) modifier la couleur de fond.

left(angle) Tourner à gauche d’un angle donné (exprimé en degrés)

right(angle) Tourner à droite

width(épaisseur) Choisir l’épaisseur du tracé

write(texte) Ecrire du texte

Exercice 1:

Ecrivez un programme triangle.py qui affiche un triangle équilatéral en utilisant une boucle while. Ecrivez également un programme carre.py qui affiche un carré.

Exercice 2:

Créez un fichier nommé labyrinthe.py qui réalise le dessin ci-dessous.

Pour obtenir ce dessin, on peut observer qu'il est constitué de 2 segments perpendiculaires de longueur 10, puis de 2 segments perpendiculaires de longueur 20, puis de longueur 30, et ainsi de suite.

Exercice 3:

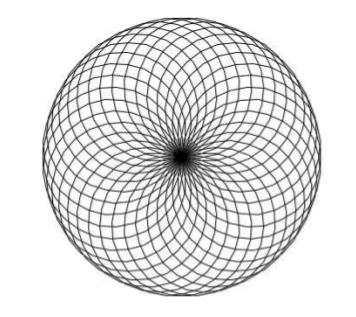
Créez un fichier nommé cercle.py et réalisant le dessin ci-dessous. Pour obtenir ce dessin, on peut remarquer qu'il est constitué de cercles de même rayon, avec un décalage de 10 degrés entre deux cercles successifs (soit 36 cercles au total). On utilisera bien évidemment une boucle...

Exerice 4:

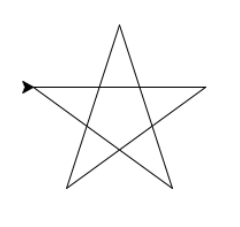
Essayez de réaliser l'étoile suivante :

Exercice 5:

Essayez de réaliser de beaux dessin ! Vous pourrez vous inspirer des dessins présentés ci-dessous.